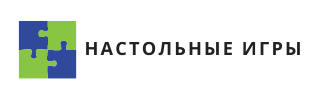Почему СОПРОТИВЛЕНИЕ лучше других игр для компании
В сравнении с другими играми у Сопротивления множество преимуществ.
- в отличие от Мафии, выбывшие игроки не скучают. Их просто нет
- В отличие от Мафии, нет долгих фаз «закрытия-открытия глаз»
- В отличие от Bang игра не требует компонентов. И Bang заточен до 7 игроков.
- В отличие от Alias здесь нет разделения на команды и сильной зависимости от интеллекта игроков.
- В отличие от SPYFALL, это не словесно-психологическая игра, где шпиона можно вычислить по неуверенности или ошибке.
- В отличие от Переворота, здесь не нужны специальные компоненты
Любой сюжет можете натянуть на игру! Будь то звездные войны, Сайлоны в Battlestar Galactica, Харконнены в рядах Атрейдесов на Дюне, или даже переворот коммунистов в 1917 году с контрреволюционерами в рядах Ленина!
Вы можете сделать игру в стиле «План пятилетки»! Вы — колхозники и ваша цель — успешно засеять три поля кукурузы и выполнить план товарища Сталина. Главный становиться председателем колхоза, а Шпионы — тунеядцами, которые срывают план посевов
Сопротивление проводника
Сопротивление проводника напрямую зависит от его геометрических размеров, а также материала изготовления. Меньшее сопротивление протеканию электрического тока будет оказывать проводник более толстого сечения и меньшей длины. Математически это выглядит следующим образом:
R = p l/S
- R – электрическое сопротивление проводника, Ом.
- p – удельное сопротивление проводника, Ом·мм2/м.
- l – длина проводника, м.
- S – площадь сечения проводника, м2.
Самыми меньшими удельными сопротивлениями обладают:
- серебро – 0,016 Ом·мм2/м;
- медь – 0,0175 Ом·мм2/м;
- золото – 0,023 Ом·мм2/м;
- алюминий – 0,029 Ом·мм2/м.
Наибольшие удельные сопротивления у графита – 13 Ом·мм2/м, фарфора – 1019 Ом·мм2/м, эбонита – 1020 Ом·мм2/м.
§ 45. Расчёт сопротивления проводника. Удельное сопротивление
Мы знаем, что причиной электрического сопротивления проводника является взаимодействие электронов с ионами кристаллической решётки металла (§ 43). Поэтому можно предположить, что сопротивление проводника зависит от его длины и площади поперечного сечения, а также от вещества, из которого он изготовлен.
На рисунке 74 изображена установка для проведения такого опыта. В цепь источника тока по очереди включают различные проводники, например:
- никелиновые проволоки одинаковой толщины, но разной длины;
- никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения);
- никелиновую и нихромовую проволоки одинаковой длины и толщины.
Силу тока в цепи измеряют амперметром, напряжение — вольтметром.
Зная напряжение на концах проводника и силу тока в нём, по закону Ома можно определить сопротивление каждого из проводников.
Рис. 74. Зависимость сопротивления проводника от его размеров и рода вещества
Выполнив указанные опыты, мы установим, что:
- из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление;
- из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока, поперечное сечение которой меньше;
- никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.
Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, впервые на опытах изучил Ом. Он установил, что сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.
Как учесть зависимость сопротивления от вещества, из которого изготовляют проводник? Для этого вычисляют так называемое удельное сопротивление вещества.
Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной 1 м, площадью поперечного сечения 1 м2.
Введём буквенные обозначения: ρ — удельное сопротивление проводника, I — длина проводника, S — площадь его поперечного сечения. Тогда сопротивление проводника R выразится формулой
Из неё получим, что:
Из последней формулы можно определить единицу удельного сопротивления. Так как единицей сопротивления является 1 Ом, единицей площади поперечного сечения — 1 м2, а единицей длины — 1 м, то единицей удельного сопротивления будет:
Удобнее выражать площадь поперечного сечения проводника в квадратных миллиметpax, так как она чаще всего бывает небольшой. Тогда единицей удельного сопротивления будет:
В таблице 8 приведены значения удельных сопротивлений некоторых веществ при 20 °С. Удельное сопротивление с изменением температуры меняется. Опытным путём было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.
Таблица 8. Удельное электрическое сопротивление некоторых веществ (при t = 20 °С)
Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.
При проводке электрических цепей используют алюминиевые, медные и железные провода.
Во многих случаях бывают нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы 8, сплав нихром имеет удельное сопротивление почти в 40 раз большее, чем алюминий.
Фарфор и эбонит имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток, их используют в качестве изоляторов.
Вопросы
- Как зависит сопротивление проводника от его длины и от площади поперечного сечения?
- Как показать на опыте зависимость сопротивления проводника от его длины, площади поперечного сечения и вещества, из которого он изготовлен?
- Что называется удельным сопротивлением проводника?
- По какой формуле можно рассчитывать сопротивление проводников?
- В каких единицах выражается удельное сопротивление проводника?
- Из каких веществ изготавливают проводники, применяемые на практике?
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r – Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС (≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.
Изменения проводника при увеличении длины
Во время испытаний замечено, что при увеличении длины проводника его электрическое сопротивление увеличивается. Для проведения эксперимента, необходимо выбрать заготовки из одинакового материала. К примеру, это может быть проволока из никелина. Для считывания параметров используется амперметр, который подключен к зажимам.
Устанавливая заготовки меньшей длины, отмечено, что ток в цепи увеличивается. Даже на одном изделии можно поиграться с амперметром. Поставив щуп на середину заготовки, к примеру, может отображаться значение 50 ампер.
 Показатель амперметра
Показатель амперметра
Интересно! Если отводить его в сторону, к краю, чтобы увеличить дальность держателя, показатель тока будет снижаться. Тоже самое, касается проводников из других материалов.
Проверка диодов мультиметром или тестером
Полупроводниковые диоды широко применяются в электрических схемах для преобразования переменного в постоянный ток, и обычно при ремонте изделий, после внешнего осмотра печатной платы в первую очередь проверяют диоды. Диоды изготавливают из германия, кремния и других полупроводниковых материалов.

По внешнему виду диоды бывают разной формы, прозрачные и цветные, в металлическом, стеклянном или пластмассовом корпусе. Но они всегда имеют два вывода и сразу бросаются в глаза. В схемах в основном применяются выпрямительные диоды, стабилитроны и светодиоды.
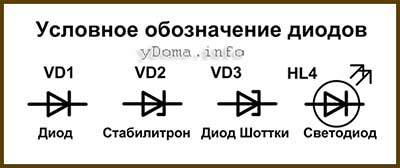
Условное обозначение диодов на схеме представляет собой стрелку, упирающуюся в отрезок прямой линии. Обозначается диод латинскими буквами VD, за исключением светодиодов, которые обозначаются буквами HL, В зависимости от назначения диодов в схему обозначения вносятся дополнительные элементы, что и отражено на чертеже выше. Так как в схеме диодов бывает больше одного, то для удобства после букв VD или HL добавляется порядковый номер.
Проверить диод гораздо легче, если представлять, как он работает. А работает диод как ниппель. Когда Вы надуваете мячик, резиновую лодку или автомобильное колесо, то воздух в них входит, а обратно его не пускает ниппель.
Диод работает точно также. Только пропускает в одну сторону не воздух, а электрический ток. Поэтому для проверки диода нужен источник постоянного тока, которым и может служить мультиметр или стрелочный тестер, так как в них установлена батарейка.
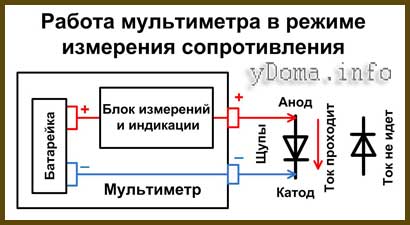
Выше представлена структурная схема работы мультиметра или тестера в режиме измерения сопротивления. Как видно, на клеммы подается напряжение постоянного тока определенной полярности. Плюс принято подавать на красную клемму, а минус на черную. При прикосновении к выводам диода таким образом, что плюсовой выход прибора окажется на анодном выводе диода, а минусовой на катоде диода, то ток через диод пойдет. Если щупы поменять местами, то диод ток не пропустит.
Диод обычно может иметь три состояния – быть исправным, пробитым или в обрыве. При пробое диод превращается в отрезок провода, будет пропускать ток при любом порядке прикосновении щупов. При обрыве напротив, ток не будет идти никогда. Редко, но бывает и еще одно состояние, когда изменяется сопротивление перехода. Такую неисправность можно определить по показаниям на дисплее.
По выше приведенной инструкции можно проверять выпрямительные диоды, стабилитроны, диоды Шоттки и светодиоды, как с выводами, так и в SMD исполнении. Рассмотрим, как проверять диоды на практике.

В первую очередь необходимо, соблюдая цветовую маркировку, вставить в мультиметр щупы. Обычно в COM вставляется черный провод, а в V/R/f – красный (это плюсовой вывод батарейки). Далее необходимо установить переключатель режимов работы в положение прозвонки (если есть такая функция измерений), как на фотографии или в положение 2kOm. Включить прибор, сомкнуть концы щупов и убедиться в его работоспособности.

Практику начнем с проверки древнего германиевого диода Д7, этому экземпляру уже 53 года. Диоды на основе германия сейчас практически не выпускают из-за высокой стоимости самого германия и низкой предельной рабочей температуры, всего 80-100°С. Но эти диоды имеют самое маленькое падение напряжения и уровень собственных шумов. Их очень ценят сборщики ламповых усилителей звука. В прямом включении падение напряжения на диоде из германия составляет всего 0,129 В. Стрелочный тестер покажет приблизительно 130 Ом. При смене полярности мультиметр показывает 1, стрелочный тестер покажет бесконечность, что означает очень большое сопротивление. Данный диод исправен.
Порядок проверки кремниевых диодов не отличается от проверки сделанных из германия. На корпусе диода, как правило, помечается вывод катода, это может быть окружность, линия или точка. В прямом включении падение на переходе диода составляет около 0,5 В. У мощных диодов напряжение падения меньше, и составляет около 0,4 В. Точно также, проверяются стабилитроны и диоды Шоттки. Падение напряжения у диодов Шоттки составляет около 0,2 В.

У мощных светодиодов на прямом переходе падает более 2 В и прибор может показывать 1. Но тут сам светодиод является индикатором исправности. Если при прямом включении видно, даже самое слабое свечение светодиода, то он исправен.
Надо заметить, что некоторые типы мощных светодиодов состоят из цепочки включенных последовательно несколько светодиодов и внешне это не заметно. Такие светодиоды иногда имеют падение напряжения до 30 В, и проверить их возможно только от блока питания с напряжением на выходе более 30В и включенным последовательно со светодиодом токоограничивающим .
Полное сопротивление
При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах
Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.

Полное сопротивление представляет собой сумму активного и реактивного сопротивления в цепи переменного тока, но такое сложение необходимо выполнять особым образом. Для этого нужно начертить прямоугольный треугольник, катеты в котором должны иметь длину, равную величине активного и реактивного сопротивлений соответственно.
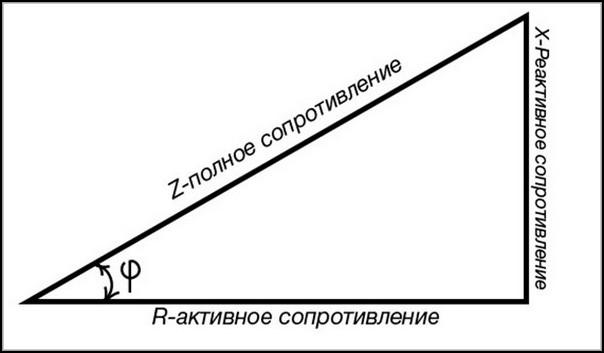
Длина гипотенузы будет численно выражать полное сопротивление электрической цепи. Для его определения используется правило, говорящее о том, что сумма квадратов катетов равна квадрату гипотенузы. Это правило называют теоремой Пифагора. Следовательно, формула, с помощью которой можно найти полное сопротивление, выглядит так:
Z = √(R^2+〖(XL-XC)〗^2 ), где
- Z — полное сопротивление;
- R — величина активной составляющей;
- XL и XC — значение индуктивного и емкостного параметра соответственно.
Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.

Линейное и нелинейное сопротивления. Обзор.
Всем добрый день, тема навеяна отсутствием понимания в некоторых расчетах и диалогах. Большинство электриков учили законы Кирхгофа 1 и 2, если такие помните.
Если первый закон больше важен для направленности токов в узле, то второй на распределение напряжения по контуру. Эти значения действуют для мгновенных значений. Те кто помнит курс ТОЭ, вспомните, что при расчете переходных процессов, одна и та же схема может рассматриваться в трех и более состояниях. В начальный момент (пуска схемы), в момент переходного процесса и в устоявшемся режиме. Но по второму закону Кирхгофа сложно подсчитать перераспределение всех напряжений в динамике, только если взять конкретный промежуток времени и его просчитать.
Это связано с тем, что в схеме присутствуют разные элементы: индуктивности, емкости, диоды, и много других.
Теперь подходим к самому главному, линейное сопротивление, может быть только у пассивных элементов, и это только резисторы.
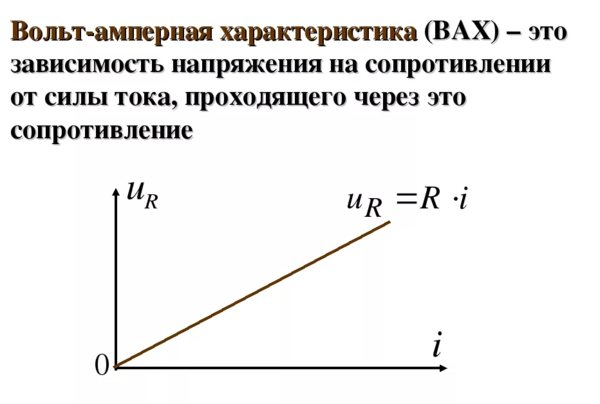
Транзистор или диод имеют в своих ВАХ линейные участки, но сами их характеристики нелинейные.
То есть на самом деле подсчет тока или напряжения в конкретной схеме, можно рассчитать только примерно или опытным путем.
Лампа накаливания — нелинейный элемент, так как сопротивление нити накала зависит от температуры. Спираль утюга — аналогично. Обмотки двигателя вообще имеют активное сопротивление меньше ома, но там есть индуктивная составляющая.
К чему все эти пояснения, к тому что в реальных условиях Вы не найдете сегодня схемы с чистым линейным сопротивлением. И если написано, что мощность, 100 Вт, то при напряжении в 12 вольт, будет ток в цепи 100/12= 8,33 А. А при напряжении в 14 вольт ток будет 7,14 А. Это совсем неверно, так как есть схемы стабилизации корректирующие работу.
Для светодиодов, например, для свечения важен сам факт протекания тока определенного номинала. И как правило на характеристиках драйверов (блоков питания ) пишут, на какой ток прежде всего ориентирован драйвер.
Так же есть схема стабилизации, которая будет держать заданный ток или напряжение, независимо от напряжения питания. Это касается не только светодиодной ленты, а многих других современных устройств имеющие в составе электронные платы.
Получилось немного сложно, но основная идея думаю понятна.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
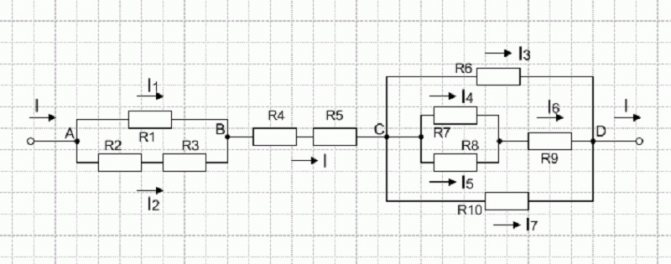
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения
Делают расчёты для каждого такого звена, после – всей цепи целиком
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
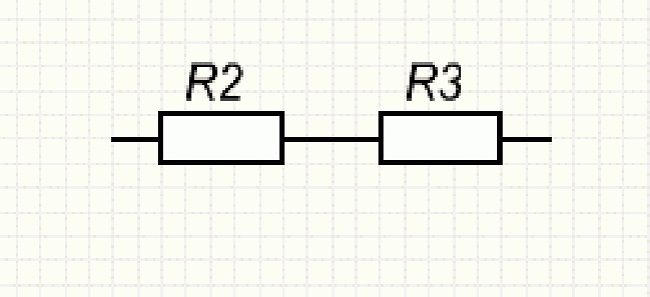
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
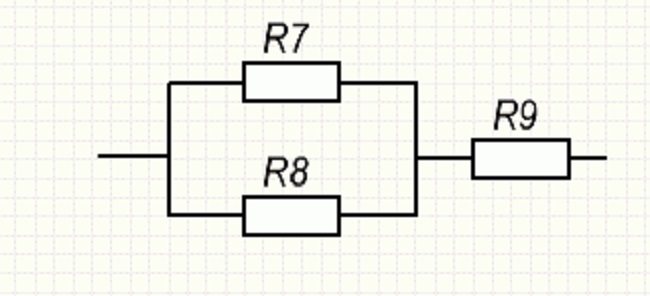
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
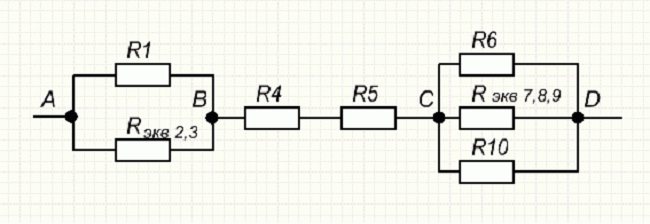
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
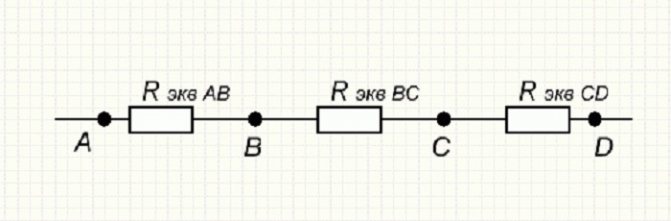
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Список выпусков и участников
В столбце списка участников полужирным отмечены игроки, которые были лидерами в каждой из группировок (Главарь и Убийца), курсивом отмечен Журналист.
| № | Дата показа | Сопротивление | Шпионы | Кто победил |
|---|---|---|---|---|
| 1 | 2 декабря 2016 | Станислав БагровАнатолий ОвчинниковДмитрий ЯковлевАндрей Багров | Алексей ГорбулевРоман ТранцевДмитрий Данилович | Сопротивление |
| 2 | 16 декабря 2016 | Рамиль ГайнуллинКирилл ХлопинОлег КовалевАнвар Насриддинов | Северин СтукасКирилл АлексеевМихаил Комиссаров | Шпионы |
| 3 | 30 декабря 2016 | Роман ТранцевВладимир КаркоцкийВадим ГолунгаВадим Иванов | Дмитрий ДаниловичВладислав ПрокофьевАндрей Балабанов | Шпионы |
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 – 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 – 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
Олово | 0,12 |
Платина | 0.107 |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 – 0,137 |
Титан | 0,6 |
Хромаль | 1,3 – 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
| Закон Ома для полной цепи I = ε/(R + r) I — сила тока ε — ЭДС R — сопротивление r — внутреннее сопротивление источника |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Что в наборе?
В комплекте настольной игры Сопротивление вы найдете:
- Десять карт персонажей. Одного из них вы получите в начале. Все личности имеют различные характеристики и свои способности.
- Жетон лидера, который определит главного в вашей команде сопротивления.
- Пять командных жетонов. Они понадобятся, чтобы отмечать группы, участвующие в выполнении миссии.
- Двадцать жетонов, чтобы высказать свое мнение о миссии. Десять фишек говорят “за” состав, остальные – против.
- Десять карточек со статусом прохождения миссии. Пять из них означают успешное прохождение задания, оставшиеся пять – провал.
- Пятнадцать вариантов сюжета для разнообразия в противостоянии властям.
- Пять фишек с двумя сторонами, которые обозначают итоги миссии: провал или выполнение.
- Три специальных поля, чтобы подсчитать результат игры и понять смогли ли ополченцы свергнуть власть.
- Жетон голосований, чтобы отследить сколько раз участники сопротивления успели высказать свое мнение в игре.
- Фишка текущий миссии, чтобы отслеживать прогресс ее выполнения.
- Коллекционный магнит-подарок от издательства игры.
Сопротивление правила на русском языке с полным описанием механики игры.
Как найти сопротивление в цепи?
Его можно узнать из закона Ома, который связывает силу тока, напряжение и сопротивление. В этом случае, оно рассчитывается по формуле
формула сопротивления через закон Ома
где
R — сопротивление, Ом
U — напряжение на концах проводника, Вольты
I — сила тока, текущая через проводник, Амперы
То есть нам достаточно замерить напряжение на концах какого-либо проводника и измерить силу тока, проходящую через него. После применить формулу и рассчитать сопротивление проводника. Давайте для закрепления решим простую задачу.
Задача
Рассчитать сопротивление проводника, если известно, что на него подают напряжение 5 Вольт и сила тока, проходящая через него 0,1 Ампер.
Решение
Используем формулу
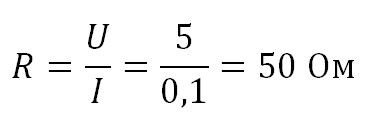

постоянные резисторы
Также вот вам видео, где очень умный преподаватель объясняет, что такое сопротивление
Близкие темы к этой статье